
モンティ・ホール問題をわかりやすく図解付きで説明している。
今まで、モンティ・ホール問題に納得できなかった人に見てもらいたい。
モンティ・ホール問題とは
モンティ・ホール (Monty Hall、本名 Monte Halperin) が司会者を務めるアメリカのゲームショー番組、「Let’s make a deal」の中で行われたゲームに関する論争に由来する。
モンティ・ホール問題
モンティ・ホール問題とは、確率論の有名な問題の一つ。
問題の内容自体は単純明快であるものの、「直感的な答えと、きちんと確率論に則って導き出された答えが異なる」という人が後を絶たない。
モンティ・ホール問題とは (モンティホールモンダイとは)
モンティ・ホール問題の内容
実際にどんな問題なのか見てみよう
(2) プレーヤーは箱を1つ選ぶ。
(3) 出題者は残りの箱のうち1つを”必ず”開ける。
(4) 出題者の開ける箱は、”必ず”ハズレの箱である。
(5) 出題者はプレーヤーに箱を選び直すチャンスを”必ず”与える。
(6) 最初と違う箱を選んだ場合、アタリの確率は2/3である。
よくある勘違い
確率は1/3
出題者が箱を開けようが最初から確率は1/3のまま。
選び直す意味はない。
確率は1/2
出題者が1つ箱を開けたため箱は2個。
どちらを選んでも確率は1/2なので、選び直す意味はない。
モンティ・ホール問題の解説
本当に確率は2/3なのか?
実際にA(アタリ),B(ハズレ),C(ハズレ)の箱を順番に選んで確率を見てみよう。

「最初にA(アタリ)を選択した場合」
残ったもう1つの箱は必ずハズレである。
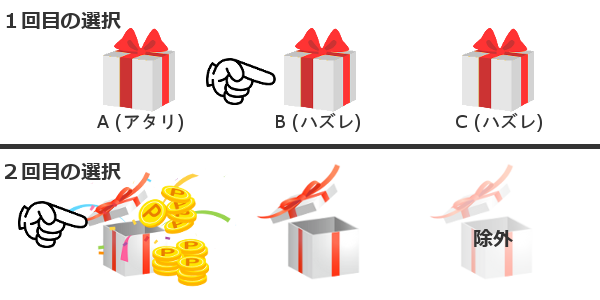
「最初にB(ハズレ)を選択した場合」
残ったもう1つの箱は必ずアタリである。
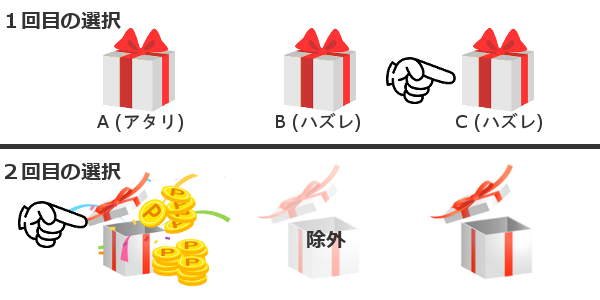
「最初にC(ハズレ)を選択した場合」
残ったもう1つの箱は必ずアタリである。
2回目に箱を変えることで、アタリを選ぶ確立は2/3であることがわかってもらえただろうか。
2回目の選択肢の意味を考える
1回目と2回目の選択肢を切り離して考えれば、
2回目の選択肢でアタリを選ぶ確立は1/2
となり、先ほど述べた”勘違い”をしてしまう。
しかし、実際は2回の選択権が与えられ
1回目の選択により、2回目の選択に影響を与えている。
2回目の選択肢で
箱を変えない場合、アタリを選ぶ確立は1/3
箱を変えた場合、アタリを選ぶ確立は2/3
となる。
逆にハズレを選ぶ確立を考えるとわかりやすい。
最初にハズレの箱を選ぶ確立は2/3。
2回目の選択肢で、もうひとつの箱がアタリの確率も2/3※となる。
※:1/3とはならない。Aがアタリの確率が100%なら、もう1つの箱がハズレの確率は100%となる。0%ではない。
箱が10個の場合の確率

わかりやすくするために箱を10個に増やしてみよう。
最初の選択肢でアタリを選ぶ確立は1/10。
逆に、最初にハズレを選ぶ確立は9/10となる。
出題者が8個のハズレの箱を開き、プレイヤーにもう一度選択権が与えられる。
どちらかがアタリで、どちらかがハズレだ。
最初に選んだ箱が9/10の確率でハズレだから、
2回目の選択肢で、もうひとつの箱がアタリの確率も9/10となる。
最初に選ぶハズレの確立が高いほど、もうひとつの箱がアタリの確率も高くなっていく。
100個なら99/100の確率で。
1000個なら999/1000の確率で。
出題者が回答者の正解率をヒントで出さない限り外れた扉を知ってるからって開いても 当初の正答率の変更など関係ない さらには出題者が言う3分の1の確率もおかしい 出題者は人間であるならば 利き手左手ましてや中央におく不安も考慮し子供的思考でない限りぶれ それに応じた回答者 の選択率も変わる・・ 全くもって呆れるな ・・天才が天才というのを知りたい割に子供的短絡設定 横やり的な判定 IQが高いらしいが人に対するたぶらかしと見える
1⃣出題者の開ける箱は、”必ず”ハズレの箱である。
→ 出題の正答率は変わらない
<もともと確認していたハズレの箱にマーキングしただけで箱の数が減ったわけではない
回答者が箱を変える意味はない>
2⃣出題者が意図せず ハズレを引く
→ 改めて正答率が増える
これが正しい判断
三点申し上げます、
A
《1⃣出題者の開ける箱は、”必ず”ハズレの箱である。
→ 出題の正答率は変わらない
<もともと確認していたハズレの箱にマーキングしただけで箱の数が減ったわけではない
回答者が箱を変える意味はない>
2⃣出題者が意図せず ハズレを引く
→ 改めて正答率が増える》
まずこの回答は、このサイトもしく他のサイトで
3分の2の説明の前に自分が出したもの
数学者が数式で表現する事実
を説明なしで直感で言い当てるのが【天才】ではないか
B
1⃣も2⃣も状況同じなのになぜこうなったか ・・
出題者は当然当たりハズレわかってる ゆえに、
回答者は通常、※勧められると100パー罠<誘導>だと直感する ・・
ゆえに選べない ※冒険者はよって別
<選択を変えたのは 天才でなく人に対する危険意識のない危険な存在>
C
この問題自体どれを当てるかで釣り結局選択肢傾向で判断とか詐欺行為に相当する・・
主題者は全ハズレともいいかねん
<IQ高い=人間を罠にはめ直感を失わせる危険な脳>ともいえ
即刻問題自体を消すべき
以上 お付き合いくださいありがとうございました・・
いいかえると 3分の2でハズレを引く確率があった それを出題者が無断でハズレをひき2分の1に変えた ここで注意は選択を変えるという行為で当たる確率が増えたのではなく選択肢を減らしたから増えたのである ゆえに出題の根幹である天才かどうかを見分ける条件に変更宣言の項目は存在しない